Quick Sort 알고리즘
기술 면접때, 퀵 정렬에 대하여 물어보았을 때, 제대로 기억이 나지 않아 헛소리 한 경험이 있어, 리마인드 차원에서 요약하려고 한다.
Pivot 위치(Left, Right, Middle)에 따른 구현은 (github)[https://github.com/moon1z10/Algorithms/blob/master/Sort/Quick%20Sort/src/QuickSort.java] 참고
퀵 정렬(Quick Sort)은 정렬 알고리즘 중 하나로, 평균적으로 매우 빠르고 효율적인 성능을 보여주는 알고리즘입니다.
정의
퀵 정렬은 분할 정복(Divide and Conquer) 방법을 사용하여 리스트를 정렬하는 알고리즘입니다. 퀵 정렬은 주어진 리스트를 피벗(pivot)이라는 기준 요소를 중심으로 두 부분으로 나누고, 각각의 부분 리스트를 재귀적으로 정렬하여 전체 리스트를 정렬합니다.
정렬하는 방법
퀵 정렬의 정렬 과정은 다음과 같습니다:
- 피벗 선택: 리스트에서 하나의 요소를 선택하여 피벗으로 설정합니다. 피벗 선택 방법은 여러 가지가 있으며, 일반적으로 첫 번째 요소, 마지막 요소, 중앙 요소, 또는 랜덤 요소를 선택할 수 있습니다.
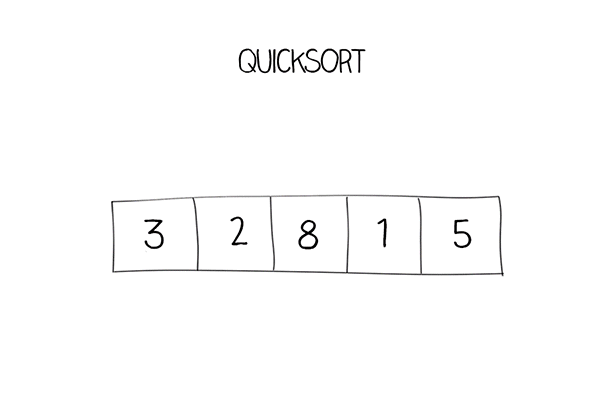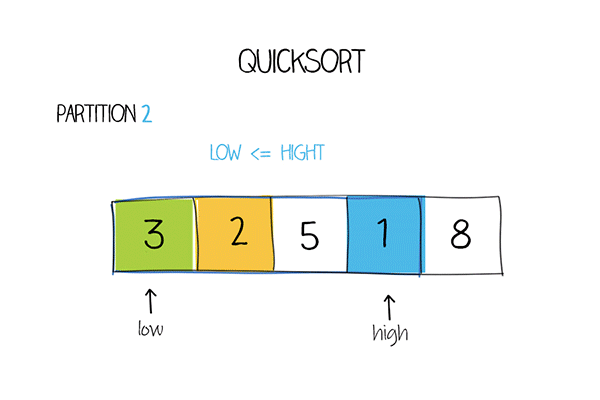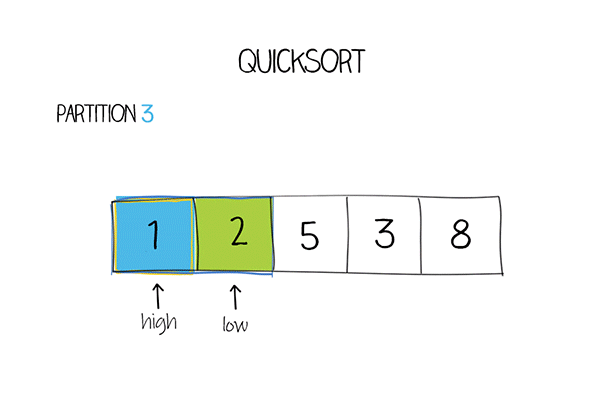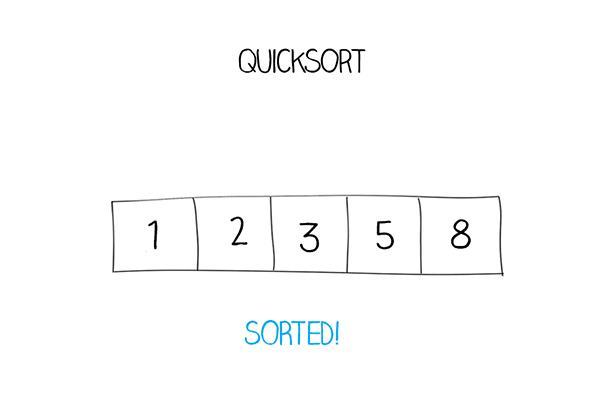
- 분할: 리스트를 피벗을 기준으로 두 개의 부분 리스트로 나눕니다. 피벗보다 작은 요소들은 왼쪽 부분 리스트에, 피벗보다 큰 요소들은 오른쪽 부분 리스트에 위치하게 합니다.
- 재귀적 정렬: 분할된 두 부분 리스트에 대해 재귀적으로 퀵 정렬을 수행합니다.
- 합병: 각 부분 리스트가 정렬되면, 피벗과 함께 합쳐서 전체 리스트를 정렬합니다.
왜 O(nlogn)을 보장하는지
퀵 정렬이 평균적으로 O(nlogn)의 시간 복잡도를 보장하는 이유는 다음과 같습니다:
- 분할 과정: 퀵 정렬은 리스트를 반으로 나누는 작업을 반복합니다. 각 분할 단계는 O(n)의 시간이 소요됩니다.
- 재귀적 깊이: 이상적인 경우, 리스트는 매번 반으로 나누어지며, 이 경우 재귀 호출의 깊이는 log(n)이 됩니다.
- 총 시간 복잡도: 각 단계의 분할 작업이 O(n)의 시간이 소요되고, 이러한 단계가 log(n)번 반복되므로, 전체 시간 복잡도는 O(nlogn)이 됩니다.
최악의 경우는 어떻게 되는지
퀵 정렬의 최악의 경우 시간 복잡도는 O(n^2)입니다. 이는 다음과 같은 상황에서 발생할 수 있습니다:
- 불균형 분할: 매번 피벗이 리스트의 가장 크거나 가장 작은 요소를 선택하게 되어, 리스트가 하나의 요소와 나머지 요소들로 나누어지는 경우입니다.
- 이미 정렬된 리스트: 만약 리스트가 이미 정렬되어 있거나 역순으로 정렬되어 있는 경우, 피벗을 부적절하게 선택하면 매번 한쪽으로 치우친 분할이 발생하여 재귀 호출의 깊이가 n에 이르게 됩니다.
이러한 최악의 경우를 방지하기 위해 랜덤 피벗 선택 또는 피벗을 임의로 섞는 방법을 사용할 수 있습니다. 이를 통해 최악의 경우를 방지하고 평균적인 O(nlogn) 성능을 유지할 수 있습니다.
예시
Initial: [10, 7, 8, 9, 1, 5]
Pivot: 5
Step 1: [1, 5, 10, 7, 8, 9]
[1] [5] [10, 7, 8, 9]
Step 2: Pivot: 9
[1] [5] [7, 8, 9, 10]
[1] [5] [7, 8] [9] [10]
Step 3: Pivot: 8
[1] [5] [7] [8] [9] [10]
Final: [1, 5, 7, 8, 9, 10]
공간 복잡도 분석
퀵 정렬의 공간 복잡도는 크게 두 가지로 나누어 생각할 수 있습니다:
재귀 호출 스택의 공간:
- 퀵 정렬은 재귀적으로 구현되기 때문에, 재귀 호출 스택이 사용됩니다.
- 평균적으로 퀵 정렬의 재귀 깊이는 O(log n)입니다. 이는 리스트를 분할할 때마다 리스트가 반으로 나누어지기 때문입니다.
- 그러나 최악의 경우, 재귀 깊이는 O(n)이 될 수 있습니다. 이는 리스트가 이미 정렬되어 있거나 매우 불균형하게 분할되는 경우입니다.
추가적인 메모리 사용:
- 퀵 정렬은 주로 제자리 정렬(in-place sort)로 구현됩니다. 즉, 입력 리스트 외에 추가적인 리스트를 생성하지 않습니다.
- 따라서, 퀵 정렬은 추가적인 메모리를 거의 사용하지 않으며, 추가 메모리 사용은
O(1)입니다.
공간 복잡도의 결론
- 평균적인 공간 복잡도: O(log n) (재귀 호출 스택의 깊이)
- 최악의 경우 공간 복잡도: O(n) (재귀 호출 스택의 깊이)
따라서, 퀵 정렬은 추가적인 메모리 사용 측면에서 매우 효율적이며, 평균적으로 O(log n)의 공간 복잡도를 가집니다. 이는 리스트의 길이에 따라 재귀 호출 스택이 깊어지기 때문입니다. 하지만, 최악의 경우에는 O(n)의 공간 복잡도를 가질 수 있습니다. 이러한 경우를 방지하기 위해 랜덤 피벗 선택이나 피벗을 임의로 섞는 방법을 사용하여 최악의 경우를 줄일 수 있습니다.
구현
import java.util.Arrays;
public class QuickSort {
//Divide and conquer, Time worst O(n^2) average O(n*logn), Space O(logn), n is array length
public static void quickSort(int[] a, int low, int high) {
int index = partition(a, low, high);
if (low < index-1)
quickSort(a, low, index-1);
if (index < high)
quickSort(a, index, high);
}
//Partition, Time O(n), Space O(1)
private static int partition(int[] a, int low, int high) {
int mid = low + (high-low)/2; //middle of the array
int pivot = a[mid];
while (low <= high) {
while (a[low] < pivot)
low ++;
while (a[high] > pivot)
high --;
if (low <= high) {
swap(a, low, high);
low ++;
high --;
}
}
return low;
}
//Swap two elements by index, Time O(1), Space O(1)
private static void swap(int[] a, int i, int j) {
int tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
public static void main(String[] args) {
int[] a = {19, 33, 4 , 61, 5, 38, -36, 21, 0};
quickSort(a, 0, a.length-1 );
System.out.print("Quick sort: ");
System.out.println(Arrays.toString(a));
}
}
Leave a comment